円周率が「3」だったら、どうなる？

(2) 正六角形

円周率とは

「3.14」でおなじみの円周率とは直径に対する円周の長さを示す値です。

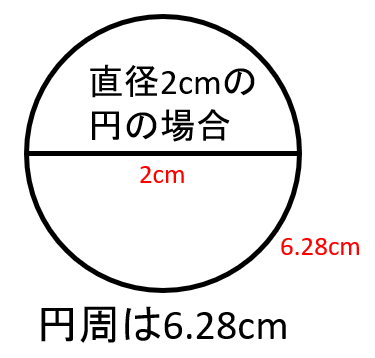
たとえば、半径1cm、直径2cmの円の円周は2×3.14＝約6.28cmになります。

円周率が「3」だったらどうなる？

仮に円周率が3だった場合、直径が2cmの円の円周は2×3＝6cmになります。これは、直径2cmの円に内接する正六角形の全辺の長さ6cmと同じになってしまいます。

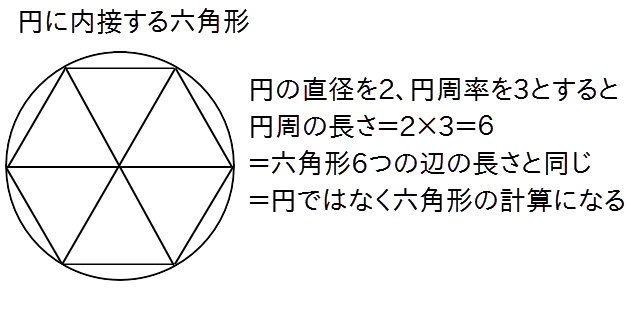つまり、円ではなく六角形について計算していることになります。

図を見てもわかるように、円周は内接する六角形の周よりも長いので、円周率は「3」よりも大きいことがわかります。

また、円周率が「4」だったら円周は直径4つ分の長さになります。これは円の外に描いた四角形の4辺の長さと同じです。

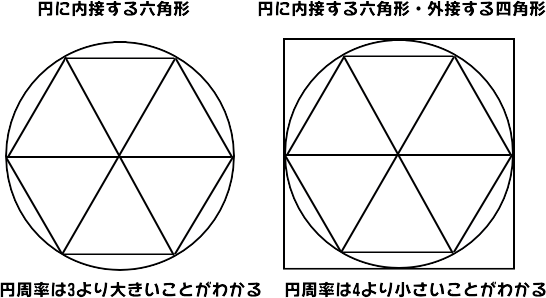
言うまでもなく円周の長さはこの長さ（円に外接する四角形の周）よりも短いので、円周率は4より小さいことがわかります。

まとめると、円周率は3より大きく4より小さいということがわかります。

さらに作業を進めていけば、3.14に近づくのではないでしょうか。

円周率の近似値

円周率に近い値となる分数で有名なのは、紀元前3世紀にアルキメデスが発見した22/7（3.14285714286…）や、5世紀に天文学者の祖沖之（そちゅうし）が発見した355/113（3.1415929203）があります。

355/113は3.141592まで一致しているので驚きですね。

この分数を発見した祖沖之は円周率が3.1415926～3.1415927の間であることも示したというのですからビックリです。

円周率は怖い数字？

円周率に並んだ数字の中には20010911（アメリカ・同時多発テロの日付を連想させる）や、20110311（東日本大震災の日付になる）も見つかるため「円周率は怖い数字だ！」と思われるかもしれませんが、そもそも円周率には膨大な数字の組み合わせが含まれるので、そのような日付を連想させる組み合わせが含まれても不思議ではない、というのが定説です。

ファインマン・ポイント

3.14から果てしなく数字が並ぶ円周率ですが、小数点以下762桁目以降に珍しく9が6個連続で並ぶ（999999）ポイントが現れます。物理学者のファインマンが「ここまで暗記した」と述べたことからファインマン・ポイントとよばれています。

このファインマン・ポイントは円周率で同じ数字が4個以上並ぶ最初の桁でもあります。

【参考】ファインマン・ポイント – Wikipedia

12個の0が並ぶポイントも発見される

2009年4月に筑波大学の研究チームがスーパーコンピュータによる計算で2兆5769億8037万桁まで求めた円周率の中で、0が12個連続して並ぶポイントがあることがわかったそうです。

【参考】円周率に関する驚くべき事実を紹介！ はやぶさの帰還にも影響？

惑星探査機「はやぶさ」が使う円周率は16桁

惑星探査機「はやぶさ」には16桁の円周率（3.141592653589793）が組み込まれており、地球帰還の軌道計算などに使われます。この精度は重要で、仮に3.14というおおざっぱな円周率が使われた場合、軌道に15万kmもの誤差が生じてしまうそうです。

【参考】朝日新聞デジタル：（数と科学のストーリー）円周率　アルキメデスは考えた – 教育

円周率の日

1年中さまざまな記念日がありますが「円周率の日」は予想通り3.14にちなんで3月14日です。円周率近似値の日もいくつかあり、たとえば、22/7にちなんだ7月22日などです。